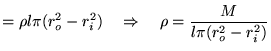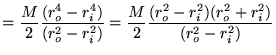Zoals je weet, of hier kunt lezen, geldt voor het traagheidsmoment van een voorwerp met dichtheid 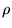$ \rho$:

$\displaystyle I = \int_V \rho r^2 \d V$ (22)

Deze integraal wordt voor een holle cilinder die draait om een lengteas door het massa middelpunt:

$\displaystyle I = \rho \int r^2 \d V = \rho \int_{r_i}^{r_o} r^2 r\d r \int_0^{2\pi}\d\theta\int_0^l \d z$ (23)

Dit uitwerken geeft:

$\displaystyle I = 2\pi l \rho \left[ \frac{r^4}{4}\right]_{r_i}^{r_o} = \frac{\pi l \rho (r_o^4-r_i^4)}{2}$ (24)

Stel dat we 2 cilinders met dezelfde massa, maar een andere binnen en buitenstraal, willen vergelijken. Dan moeten we 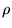$ \rho$ uit kunnen drukken in de massa $ M$:

$\displaystyle M$ $\displaystyle = \rho \int_{r_i}^{r_o} r\d r \int_0^{2\pi}\d\theta\int_0^l dz$ (25)
  $\displaystyle = \rho l \pi (r_o^2-r_i^2) \quad \Rightarrow \quad \rho= \frac{M}{l \pi (r_o^2-r_i^2)}$ (26)

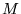Het traagheidsmoment is nu ook uit te drukken in de massa in plaats van de dichtheid:

$\displaystyle I$ $\displaystyle = \frac{M}{2} \frac{(r_o^4-r_i^4)}{(r_o^2-r_i^2)}=\frac{M}{2} \frac{(r_o^2-r_i^2)(r_o^2+r_i^2)}{(r_o^2-r_i^2)}$ (27)
  $\displaystyle = \frac{M}{2} (r_o^2+r_i^2)$ (28)