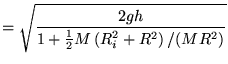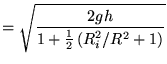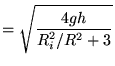Een voorwerp met een snelheid
Een voorwerp met een snelheid  heeft bewegingsenergie:
heeft bewegingsenergie:
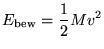 |
(1) |
Als het voorwerp roteert om een as door zijn eigen massa middelpunt (CM in het figuur, van Center of Mass), dan heeft het ook nog rotatieenergie:
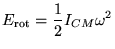 |
(2) |
Waarbij
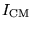 het traagheidsmoment van de cilinder om een rotatieas door het massa middelpunt, en
het traagheidsmoment van de cilinder om een rotatieas door het massa middelpunt, en  de hoeksnelheid genoemd wordt.
de hoeksnelheid genoemd wordt.
Klik hier om meer te leren over traagheidsmoment en hoeksnelheid.
 Stel we nemen een holle cilinder met buitenstraal straal
Stel we nemen een holle cilinder met buitenstraal straal  , binnenstraal
, binnenstraal 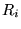 , lengte
, lengte  en massa
en massa 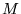 en we zetten deze cilinder bovenaan een helling met hoek
en we zetten deze cilinder bovenaan een helling met hoek  en hoogte
en hoogte  (zie de figuur hiernaast). Wanneer we de cilinder loslaten zal hij helemaal aan het begin nog stil liggen, hij heeft dan alleen maar potentiele energie, gelijk aan:
(zie de figuur hiernaast). Wanneer we de cilinder loslaten zal hij helemaal aan het begin nog stil liggen, hij heeft dan alleen maar potentiele energie, gelijk aan:
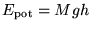 |
(3) |
waar 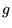 de zwaartekrachtsversnelling is (op de aarde is deze ongeveer
de zwaartekrachtsversnelling is (op de aarde is deze ongeveer
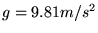 ). Wanneer deze cilinder gaat rollen, zal hij potentiele energie verliezen en bewegings- en rotatieenergie winnen. Onderaan de helling is alle potentiele energie omgezet in bewegings- en rotatieenergie. Omdat er in dit proces (als we wrijving verwaarlozen) geen verlies van energie mag optreden, kun je dan opschrijven:
). Wanneer deze cilinder gaat rollen, zal hij potentiele energie verliezen en bewegings- en rotatieenergie winnen. Onderaan de helling is alle potentiele energie omgezet in bewegings- en rotatieenergie. Omdat er in dit proces (als we wrijving verwaarlozen) geen verlies van energie mag optreden, kun je dan opschrijven:
We hebben nog een relatie tussen  en
en  nodig om de vergelijking op te kunnen lossen. Als je aanneemt dat de cilinder niet mag slippen tijdens het rollen krijg je:
nodig om de vergelijking op te kunnen lossen. Als je aanneemt dat de cilinder niet mag slippen tijdens het rollen krijg je:
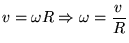 |
(5) |
Dit invullen in 5:
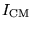 van de holle cilinder is:
van de holle cilinder is:
 |
(7) |
Voor
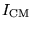 van een massieve cilinder wordt
van een massieve cilinder wordt 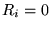 gekozen.
gekozen.
Hoe je het traagheidsmoment van een cilinder om een lengteas door het CM bepaalt, lees je hier.
Vergelijking 7 substitueren in vergelijking 6:
Het is duidelijk dat zodra 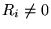 de snelheid
de snelheid  afneemt. Dus een holle cilinder is langzamer dan een massieve cilinder.
afneemt. Dus een holle cilinder is langzamer dan een massieve cilinder.
 Een voorwerp met een snelheid
Een voorwerp met een snelheid  Stel we nemen een holle cilinder met buitenstraal straal
Stel we nemen een holle cilinder met buitenstraal straal